En la figura podemos observar una esfera seccionada por un plano oblicuo en sistema diédrico. Para determinar el círculo correspondiente a su sección, hacemos por el centro de la misma una recta perpendicular a las dos trazas del plano, las dos proyecciones de esta línea perpendicular al plano son las direcciones de los ejes menores de las elipses correspondientes a la planta y alzado del círculo sección.
Los ejes mayores de las elipses en planta y alzado serán rectas perpendiculares a la recta anterior calculada. En planta tendremos que la dimensión del eje mayor de la elipse está en verdadera magnitud, pues coincide exactamente con la dimensión de la proyección del círculo en planta, que es paralela a la traza horizontal del plano. Esta misma dimensión es la que corresponde también al eje mayor de la elipse correspondiente al círculo sección en el alzado. Tenemos en consecuencia que el eje mayor de la elipse en planta es una línea horizontal, mientras que el eje mayor de la elipse en el alzado es una línea frontal. El eje menor de la elipse en planta es la proyección de la línea de máxima pendiente (aquella cuya proyección horizontal es perpendicular a la traza del plano), mientras que la proyección correspondiente al eje menor de la elipse en el alzado es la que corresponde a la línea de máxima inclinación del plano, esto es, la que es en proyección vertical perpendicular a la traza vertical del plano.
Página de secciones en sistema diédrico.
Página de secciones en sistema diédrico.
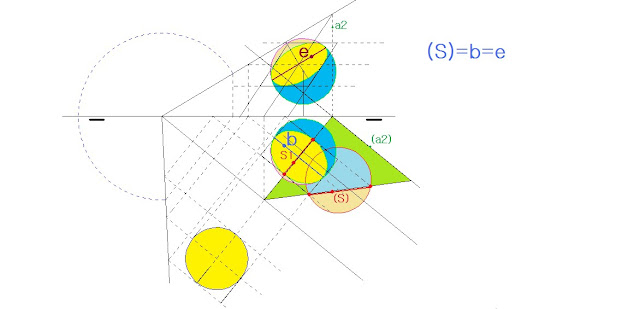
Para obtener la verdadera dimensión de la sección basta con saber que es una circunferencia cuyo diámetro es la longitud b. Podemos no obstante hacer el abatimiento del plano al pasar la longitud de un tramo de la traza del plano vertical hacia la planta, bajando por un punto por donde pasa el final de este arco una perpendicular a la línea de tierra y en este punto de intersección haciendo otra perpendicular a la traza horizontal del plano obtenemos en la intersección de la prolongación esta recta con el arco anterior el punto por donde pasa la traza vertical abatida. Para obtener el abatimiento de cada punto, es suficiente con hacer un rectángulo por cada uno de los puntos de la planta de la figura que se quieren abatir de manera que dos lados de el rectángulo se han perpendiculares a la traza horizontal del plano y los otros dos paralelos a la misma.
Sección de la esfera por cambio de plano y fundamento de la perspectiva curvilínea:
http://perspectiva-curvilinea.blogspot.com.es/
Sección de la esfera por cambio de plano y fundamento de la perspectiva curvilínea:
http://perspectiva-curvilinea.blogspot.com.es/
